

尽管服务部门通常没有直接参与生产产品或者提供服务,它们在组织运行中起着重要作用。在实践中,服务部门成本的分摊经常会给会计人员和会计专业学生们带来挫折感和恐惧感。
尽管如此,清楚、正确地理解服务部门成本在如下方面有着重要意义:首先,最为重要的是,服务部门成本被用于衡量产品的总成本;其次,它们在分配公司内部服务中也起着重要作用——免费提供的服务往往会被运营部门过度使用。另外,它们使得评估服务部门的运行效率成为可能。倘若公司内部提供的服务价格高于外部供应商,那就可以考虑取消该服务部门。
实践中,有三种方法可用于分摊服务部门成本:直接分摊法、顺序分摊法和交互分摊法。不管使用哪种分摊法,第一步都需要明确哪些部门属于运营部门,哪些部门属于服务部门。运营部门是指直接从事生产或者配送公司产品的部门,如加工和装配部门。服务部门给运营部门和其他服务部门提供服务与辅助支持,如人事和IT部门。
由于部门之间的关系错综复杂,分摊服务部门成本也相应地更加复杂。这是因为每个服务部门都有可能给所有部门提供服务,包括其他服务部门和自己部门。由于处理问题的理念不同,三种分摊法在难易程度和精确度方面都有很大差异。
直接分摊法是把成本直接分摊给各个运营部门,但不分摊给任何其他服务部门。该方法简单易行,但是忽略了服务部门之间也会相互使用服务,所以精确度较差。
顺序分摊法(也叫梯形分摊法)是把成本依次分摊给运营部门和其他服务部门,但只是单方向分摊。它没有固定的分摊顺序:通常从提供最多服务给其他部门的服务部门开始,接着按照提供服务从多到少的顺序依次把各服务部门的成本分摊给其他部门。当一个服务部门的成本分摊出去后,该部门不再接受其他服务部门成本的分摊。该方法在一定程度上考虑了和其他服务部门的关系,因此比直接分摊法更为精确。
交互分摊法充分考虑了各个服务部门,并且允许分摊成本给其他部门后,再次把成本分摊回来。因此,尽管该方法计算复杂,但也是三种方法中最精确的分摊方法。
直接分配法在20世纪70年代前被广泛使用,当时美国成本会计准则委员会(CASB)制定了分摊服务部门成本的标准。在《成本会计标准》(CAS)第418草案的“直接和间接成本的分摊”中,首次确认了交互分摊法。但是,Robert Kaplan和Anthony Atkinson在他们所著的《高级管理会计》中讲到:国防承包商抱怨“他们自己既不具备专业知识,也没有高超的计算能力实施该方法”。正是考虑到这些情况,后来才规定顺序分摊法可用于替代交互分摊法。
直接分摊法仅在计算结果接近顺序分摊法时允许使用。CAS 418规定:“对相互提供服务的间接成本池分摊成本时可以使用交互分摊法、顺序分摊法,或者能使计算结果接近这两种分摊法的计算方法”(CAS 9904.418.50)。
今天,成本会计教科书在介绍交互分摊法时使用的例子通常比较简单,包含反复迭代或者联立方程(或者两者)模拟计算每个部门的成本。一个仅涉及两个运营部门和两个服务部门的简单例子中,联立四个方程式,并可以手动解方程。而当服务部门多于两个时,教科书便建议我们使用联立方程、代数矩阵,并用电脑解方程。不幸的是,财务主管和学生们发现代数矩阵过于高深,对自己来说是一个挑战。
幸运的是,现在有一个简单的替代方法可以解决该难题,那就是使用Excel(或者其他任何具有类似功能的电子表格软件)的迭代计算功能。接下来,我们会用一个简单的例子说明迭代计算功能怎样通过多次迭代(或使用代数矩阵建立联立方程)替代手动分摊服务部门成本。该方法更适合主管们日常使用,也是解释和解决服务部门成本分摊难题的更好手段。
交互分摊法
假设有两个服务部门,S1和S2;两个生产部门,P1和P2。每个服务部门给其他三个部门提供服务。S1的直接成本是100美元,其基于500个人工工时分摊:其中,S2使用了100个;P1使用了250个;P2使用了150个。S2的直接成本是40美元,其基于1,000个机器工时分摊:其中,S1使用了500个;P1使用了100个;P2使用了400个(见图1)。
为了方便说明,我们把分摊基数由花费的小时数转化为各部门占时间总数的百分比(见图2)。为简化起见,假设S1和S2都不使用自己的服务。
循环迭代
图3显示的是循环迭代法下的交互分摊法。服务部门成本被来回往复分摊,经过几个计算回合直到摊回的成本接近“0”。第一回合,S1的成本分摊给S2,P1和P2,使用S1服务的分摊比例如图2的第8行所示;同时,S2的直接成本40美元加上从S1分摊过来的20美元,接着按照图2第9行显示的百分比分摊给S1,P1和P2。
在第二回合的计算中,S1的成本30美元(单元格C14)继续进行分摊和被分摊,直到S1还剩3美元(单元格C15)。该过程一直持续到S1的余额小到可以忽略。第六回合后,S1的余额变成了0.0003美元(单元格C23)。
尽管多次分摊和被分摊充分考虑了各个部门之间的交互关系,但当涉及多个服务部门时,这种计算方法既冗长又不好操作。
代数矩阵
一个更加精妙的方法是使用联立方程和代数矩阵建立交互关系模型后,然后分摊服务成本,这样就不需要多个回合的分摊计算。这种方法将使用图2中第8行和第9行的百分比建立线性方程。四个方程如下:
1.P1=0.5(S1)+0.1(S2)
2.P2=0.3(S1)+0.4(S2)
3.S1=0.5(S2)+100
4.S2=0.2(S1)+40
方程式1和2表示分摊给P1和P2的成本。P1被分摊到S1成本的50%和S2成本的10%,P2被分摊到S1成本的30%和S2成本的40%。方程式3和4表示S1和S2交互分摊得到的成本。S1被分摊到S2成本的50%和自己的直接成本100美元,S2被分摊到S1成本的20%加上自己的直接成本40美元。
手动解这四个联立方程相对而言比较简单,但随着部门数量的增加,使用电脑解代数矩阵会更加方便。在各矩阵记号中,联立方程为AX=B,其中A为4行4列的矩阵系数,X为分配给其他部门的成本,B为从服务部门分摊到的成本。等式两边同时左乘A的逆,则可得X=A-1B。
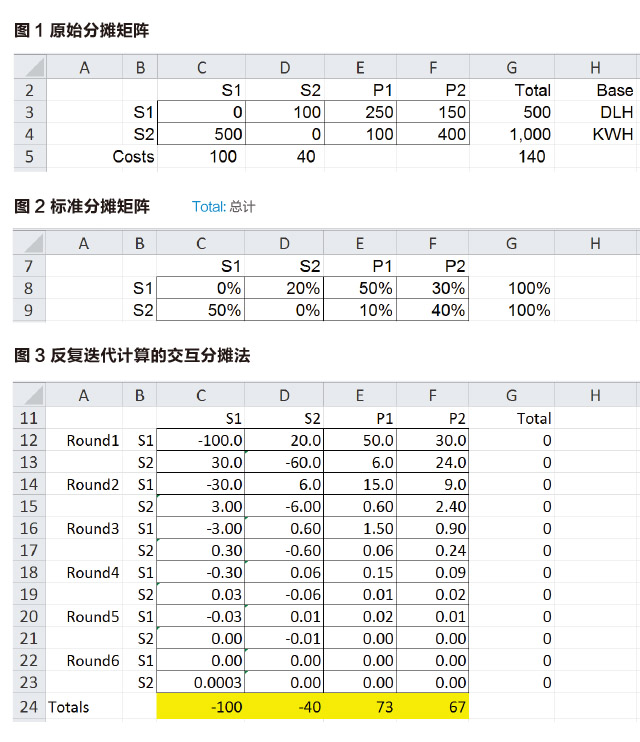
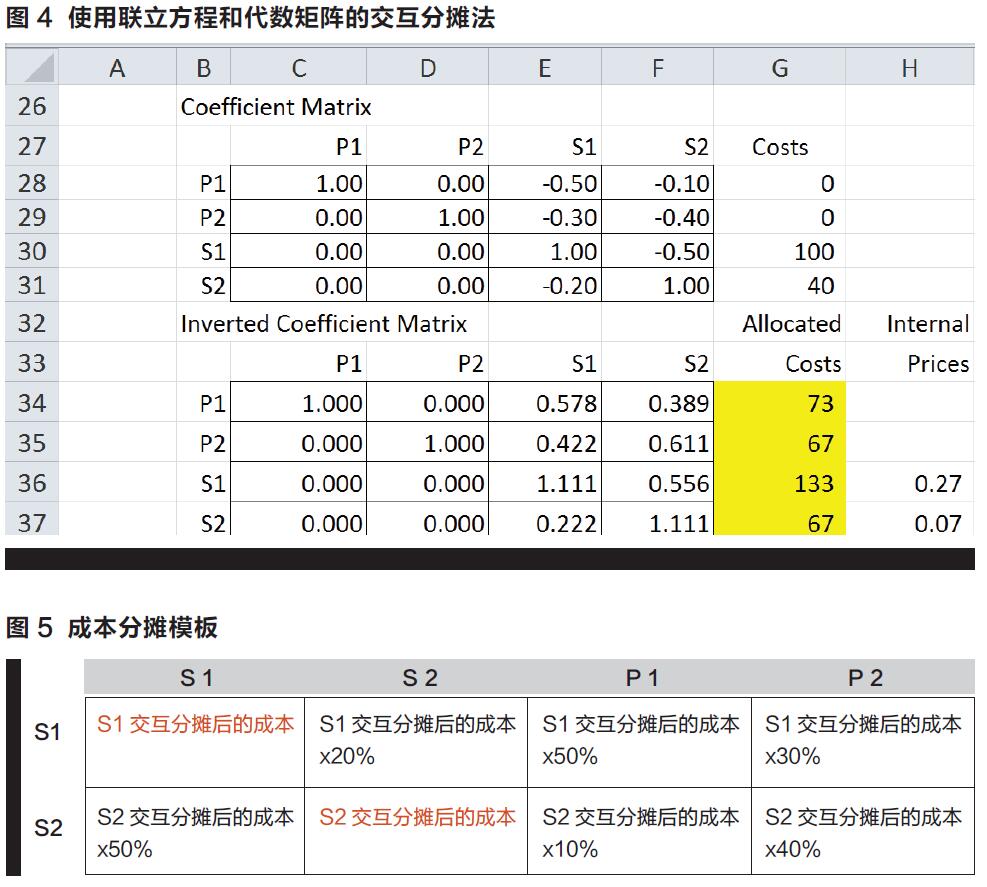
Excel的数组函数功能可以用于矩阵求逆(MINVERSE)和矩阵乘法(NMULT)。在图4中,系数矩阵为单元格C28:F31,逆系数矩阵为单元格C34:F37,分配的成本显示在单元格G34:G37。注意,分配给P1和P2的成本与反复迭代计算的交互分摊法的计算结果是一样的。但是我们前面也提到过,会计人员和会计专业学生们经常拒绝使用代数矩阵,因为他们觉得难度太大。分摊给S1和S2的成本是交互分摊而得的,它们大于S1和S2的直接成本,这是因为有一部分成本被反摊回来了。
迭代计算功能
我们在前面说过,交互分摊法需要多次重复迭代计算,并且当更多部门参与分摊时计算将变得非常繁琐。我们上面那个简单的例子中仅仅有两个部门,这都需要6个回合的计算。当计算回合再增多的时候,这种方法就欠缺实操性。但如果使用Excel的“迭代计算”功能和成本分摊模板,就可以让Excel自动进行更多回合的计算。
启用迭代计算功能后,Excel将允许公式的循环引用。循环引用是指一个单元格内的公式引用了这个公式本身所在的单元格。通常,Excel不能用于循环引用计算,因为显然计算将变得无限,就像无限循环(go-to loop)程序,会无法停止运行。而迭代计算功能允许设定重复计算的次数。
想要获得此功能,我们可以去Excel功能目录中选择公式。(以Excel 2013为例,选择“文件”—“选项”,点击“选项”下面的“公式”)在“计算选项”下选择“启用迭代计算”。而迭代计算默认的“最多迭代次数”和“最大误差”刚好符合我们这里的计算要求。
当迭代计算功能被启用后,可在模板内的单元格内输入公式,用于计算分摊成本(见图5)。首先,我们创建用来计算S1和S2交互分摊成本的公式。分摊后S1的交互分摊成本等于S1原来的直接成本加上其他服务部门分摊给S1的成本。S2的交互分摊成本等于S2原来的直接成本加上其他服务部门分摊给S2的成本。接着,再把交互分摊后的成本分摊给其他部门。
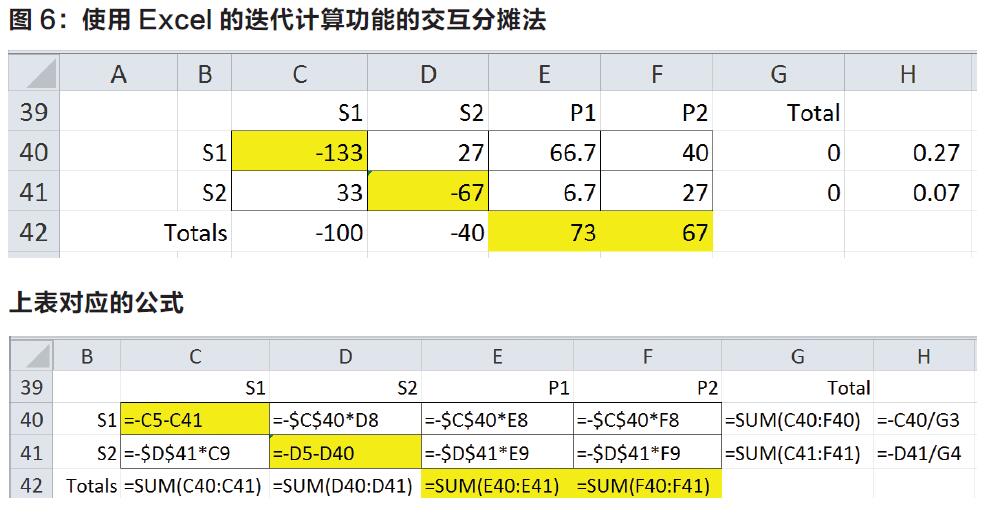
图6展示了计算结果。S1的交互分摊成本为S1原来的直接成本(100美元)和从S2分摊到的成本(33美元)。因此,单元格C40=-C5-C41。同样,S2的交互分摊成本为S2原来的直接成本(40美元)加上从S1分摊来的的成本(27美元)。单元格D41=-D5-D40。(如果迭代计算功能没有被激活,当输入这些公式后,Excel会提示“循环引用错误”的警告。)交互分摊而得的成本如果是负值,则表明是从S1和S2分摊出去的成本。
模板内其他单元格的计算方法为:用图2第8行和第9行中的百分比乘以交互分摊成本(单元格C40和C41)。用S1的交互分摊成本(133美元)乘以S1所在行的百分比(20%,50%,30%)。单元格D40,E40和F40内的公式分别为=C40*D8,=C40*E8和=C40*F8。同样地,用S2的交互分摊成本(67美元)乘以S2所在行的百分比(50%,10%,40%)。单元格C41,E41和F41内的公式分别为=D41*C9,=D41*E9和=D41*F9。这些数值为正值表明交互分摊的成本被分摊到了这些部门。通过此方法计算得出的S1和S2的交互分摊成本以及分摊到P1和P2的成本与其他方法计算出来的结果相同。
一个更简便的方法
但是这种计算方法也有缺陷。使用联立方程和代数矩阵计算交互分摊成本可以提供更多的信息,但这些信息无法从我们建议的方法中得到。例如,逆系数矩阵的主对角线上的系数(循环因子),在考虑是否外包服务部门时,可以用来计算能够节省的总变动成本。这样的信息不能从我们介绍的方法中得到,因此如果需要此类信息,就必须使用代数矩阵建立联立方程。
但是,S1和S2的交互分摊成本与分摊基数相除后可以得出内部价格。通过计算,我们不难得出S1的内部价格为0.27美元/直接人工工时($133.3/500),S2的内部价格为0.07美元/机器工时($66.7/1,000)。假设这里分析的所有成本都是变动成本,这些价格可以和外部提供同等服务的供应商的价格比较,也可以作为衡量服务部门效率的标杆。
尽管存在不足,财务经理们还是觉得此方法可使交互分摊服务部门的成本变得更加便捷。就像国防承包商拒绝CASB的建议而不愿使用交互分摊法一样,今天许多会计专业学生也觉得代数矩阵和联立方程这种方法难以应用。该方法需要建立联立方程、系数矩阵,矩阵求逆以及矩阵乘法来分摊成本。即使可以使用Excel求解矩阵,但只要谈到代数矩阵,学生们就开始大眼瞪小眼,更不用说实际使用Excel的矩阵公式(数列)时带来的额外复杂性了。使用顺序分摊法会有大量重复计算,非常繁琐。没有人希望用电子表格设置多回合的计算只为分摊成本。Excel的迭代计算功能使交互分摊法变得更加简便、快捷。
David Christensen,CMA、博士,美国南犹他大学会计系教授,IMA盐湖地区分会成员。联系方式:christensend@suu.edu。
Paul Schneider,美国南犹他大学会计系讲师。联系方式:paulschneider@suu.edu。
赵晓庆 译,李小刚 校

